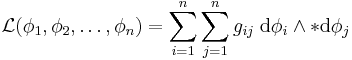Sigma model

In physics, a sigma model is a physical system that is described by a Lagrangian density of the form:

$\mathcal{L}(\phi_1, \phi_2, \ldots, \phi_n) = \sum_{i=1}^n \sum_{j=1}^n g_{ij} \; \mathrm{d}\phi_i \wedge {*\mathrm{d}\phi_j}$

Depending on the scalars g_ij it is either a linear sigma model or a non-linear sigma model. The fields 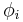$\phi_i$ , in general, provide a map from a base manifold called the worldsheet and a target (Riemannian) manifold that is often understood to be the spacetime.

A basic example is provided by quantum mechanics which is a quantum field theory in one dimension. It's a sigma model with a base manifold given by the real line parameterizing the time (or an interval, or the circle, etc.) and a target space that is the real line.